Discovering new materials and understanding the properties of existing materials are critical when addressing national security needs. To do this, Sandia studies molecular and material properties at the electronic structure level. Such calculations are expensive due to system size (number of atoms or length scale), simulation time (timescale) and accuracy needed. Materials Learning Algorithms, known as MALA, is a newly developed software framework that uses machine learning (ML) to accurately predict the electronic structure of materials for previously unattainable lengths and timescales (Figure 1). MALA offers unprecedented accuracy and scale, surpassing any existing method and computing resource. In 2023, MALA was globally recognized as an R&D100 award winner for significant technological advancements in software.

Scalable electronic structure calculations are critical for a materials modeling approach that can bridge several time and length scales. However, predictive atomistic materials modeling is hampered by the costly and redundant generation of first-principles data. Large-scale molecular dynamics (MD) simulations (LAMMPS) of material behavior require accurate interatomic potentials (IAPs), such as the spectral neighbor analysis potential (SNAP), that must be fit to higher fidelity datasets. These datasets are commonly generated using density functional theory (DFT), which is complex, expensive, limited to small scales (nanometers and femtoseconds) and exhibits N³ scaling in a system size where N is the number of atoms (see Figure 2a). The amount of data needed to construct an IAP increases exponentially with the number of chemical elements, thermodynamic states, phases and interfaces. Despite its limitations, DFT remains the most heavily used approach for electronic structure calculations and has increased in popularity since its creator won a Nobel prize in 1998.

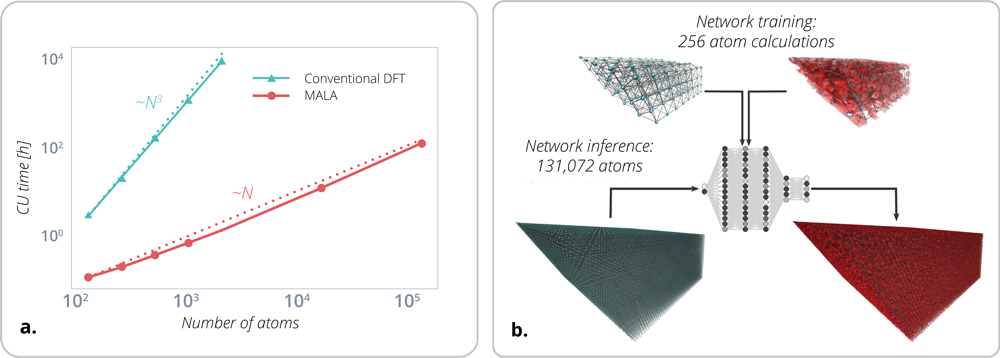
MALA addresses the issue of scaling by using a combination of ML and novel physics-based methods to enable research that was previously unfeasible. By predicting local quantities of interest with ML and computing global quantities of interest with physics-based approaches, MALA balances the trade-off between accuracy and speed. Unlike conventional methods, large MALA calculations can be distributed over multiple processors in a straightforward way, so that the time to solution is independent of the system (number of atoms) and grid sizes. One can learn the physics of the systems with just a few atoms and compute the electronic structure for much larger systems without the loss of chemical accuracy (see Figure 2b). Moreover, this approach is unique in providing both electronic structure information and total system energy. These properties uniquely position MALA to study and predict the behavior of material defects, among others, which provides fundamental physics information on the reliability of materials.

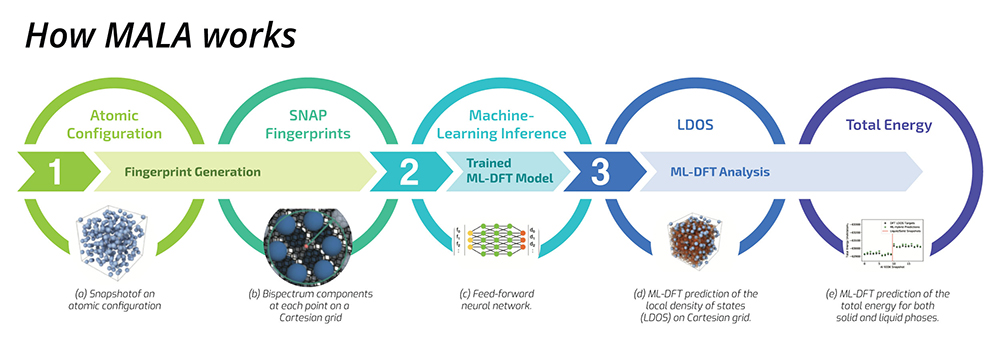
How MALA works

MALA aims to address a few key questions, namely, “Can machine learning help accelerate these first-principle electronic structure calculations?” and, “Can this be more scalable with respect to system size?” The methods developed in the MALA framework answer both questions in the affirmative. MALA employs both ML – specifically, deep neural networks (DNNs) – and physics-based approaches for predicting the electronic structure of materials. ML has become a fundamental technology for problems such as image classification, language modeling, caption generation and text or voice recognition. However, its application in the scientific domain is still in relatively early stages. While there are examples of physics-informed neural networks solving partial differential equations, applying ML to first principle calculations poses significant challenges as these calculations are the “gold standard” on which a multi-scale modeling framework is built. Surrogate models for such calculations have to be extremely accurate in order to be useful.

Instead of relying on a fully data-driven approach to understand every aspect of physics, MALA uses a hybrid approach alongside the DNN to predict local quantities of interest with very high accuracy, and a physics framework around it to compute the global quantities of interest. MALA’s grid-based approach, in which the DNN model predicts local quantities at each grid point, achieves very high accuracy while being invariant of the system size. The physics-based framework should also be able to predict system properties from the predictions of the DNN models in a scalable way. MALA’s approach to go from local density of states to quantities of interest, such as total energies, meets this requirement. These properties result in a technology that has the potential to transform multi-scale modeling methods over the next decade by surpassing the scale of traditional DFT calculations while remaining more accurate than other scalable methods. Figure 3 shows an example where stacking faults in a 131,072 atom Beryllium simulation cell were accurately predicted after training on models with 256 atoms.

MALA’s framework is a natural candidate for HPC use cases, and the DFT-based training is the classic use case for training resources at HPC facilities. Furthermore, as the system size increases, the grid size increases as well. While this results in more work (still linear in system size), the grid points can be parallelized by decomposing the grid on a supercomputer and doing independent inference at different grid points. This allows MALA’s framework to use HPC resources, especially graphics processing units (GPUs), to accelerate electronic structure calculations effectively.

Next article >