Nuclear weapon design is complex and demands that different aspects of the system are tested and analyzed to ensure their safety and reliability in different environments. One of these aspects is the system’s response to and hardening for the many potential electromagnetic environments. Additionally, the qualification of weapons in the current stockpile must be re-examined against the evolving potential electromagnetic environments in today’s world.
The testing and analysis of these systems for such environments is a vital part of Sandia’s “Always/Never” nuclear deterrence responsibility: Ensure that a nuclear weapon will always work as intended when needed and never work under any other circumstances. This assures the safety, control, and survivability of existing nuclear weapons as well as new weapons designs.
The Sandia Advanced Simulation and Computing (ASC) electromagnetics team specifically has considered this aspect of nuclear weapons stockpile qualification while developing and maintaining the EIGER and GEMMA electromagnetic ASC codes. EIGER is the legacy code, written in Fortran. GEMMA is the next generation electromagnetic simulator, written in C++ and containing additional advanced electromagnetic algorithms. Both codes have been designed to perform robust, complex assessment and analysis of nuclear weapons design and weapons qualification at Sandia while focusing on electromagnetic environments.
The team works actively with other Sandia organizations, particularly experimental electromagnetic groups. These groups provide validation data to inform code credibility and helps the team improve the code, while the code simulations can also provide feedback to experimentalists to help them plan and understand tests.
The EIGER and GEMMA codes are designed to predict the electromagnetic fields inside and outside complex nuclear weapons structures that have potential entry points. This naturally requires the code to be complex too. The team has worked for years to optimize the code so it can perform fast, high-fidelity analyses of these systems. Nevertheless, EIGER and GEMMA require the computing power of Sandia’s HPC resources as well as Los Alamos National Laboratory’s Trinity and Lawrence Livermore Laboratory’s Sierra systems.
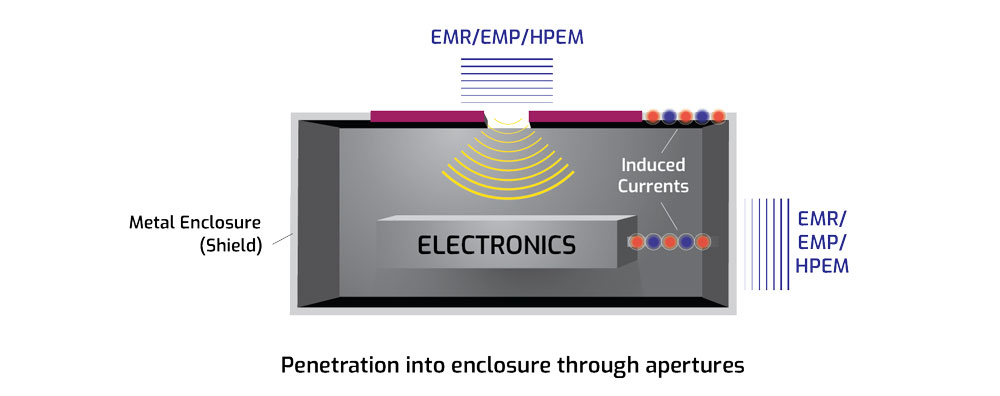
More specifically, EIGER and GEMMA simulate the major electromagnetic interference or coupling issue illustrated in Figure 1. Since electromagnetic penetration can affect internal components, it is vital for designers and analysts to understand how each specific test object is affected by such interference.
How EIGER and GEMMA work
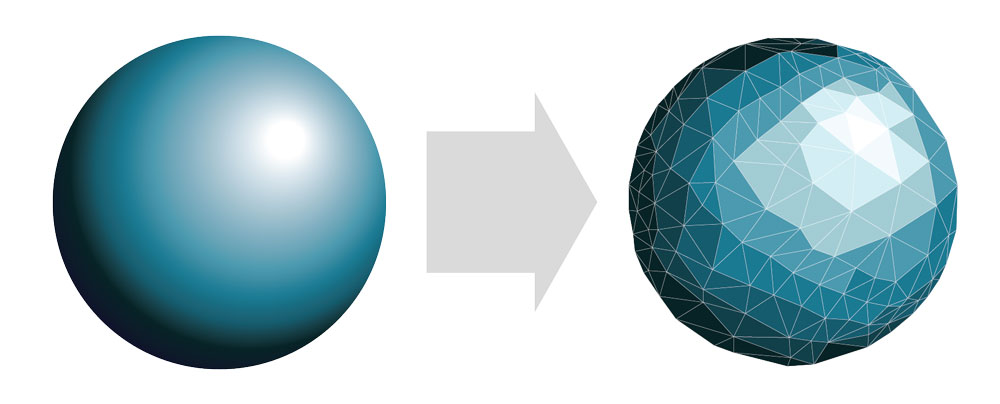
First, a three-dimensional CAD model is prepared for meshing, creating the electromagnetically-significant features and neglecting the unimportant features. Then the model is meshed with surface elements. A simple example is shown in Figure 2.
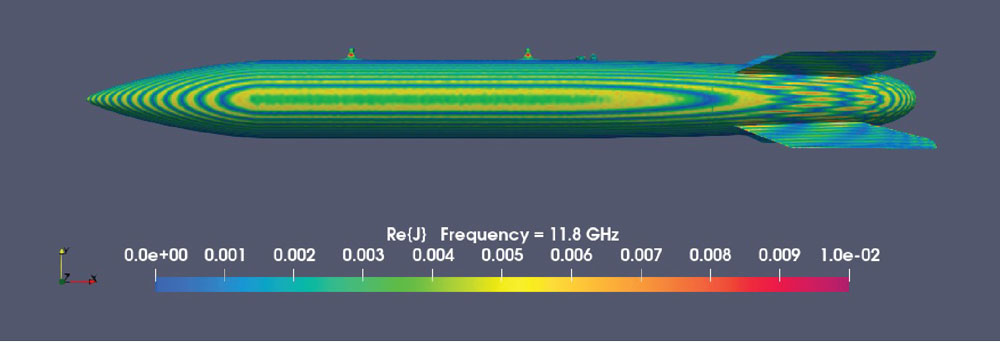
Next, a linear system is constructed by applying appropriate boundary conditions and a series of complex equations are solved for the meshed object, which include the exterior, interior and entry points. See Figure 3 for an example showing exterior currents on a B61-12.
Once the algorithms are run, the simulation results are processed to provide detailed feedback to the nuclear weapons designers and the weapons qualification engineers.
Although the above steps may seem simple, the calculations are complex and resource intensive, yet must be performed quickly and with extremely high fidelity. The complexity of these simulations depends on the object and the frequencies of the electromagnetic fields. Since more complex objects and higher frequencies require orders of magnitude more computing resources to run the EIGER and GEMMA simulations, Sandia’s HPC as well as other advanced next generation computing platforms are a key part of our “Always/Never” responsibility.
Other potential applications
Although nuclear weapon qualification is the primary mission of EIGER and GEMMA, the codes can be used in other areas, such as: electromagnetic scattering from a system by a radar, radiation from an antenna located on a system of interest, or electromagnetic effects on structures as well as components. After meshing an aircraft, the code simulations are run on an observation plane for the mesh model (see Figure 5).
After the simulation is run and analyzed, the results are mapped to show location and magnitude of the electric field on the aircraft exterior (see Figure 6).
Although EIGER and GEMMA were born from a need to qualify nuclear weapons, they can be used to understand and solve numerous other issues surrounding electromagnetic effects. GEMMA code development continues, focusing on advanced algorithms and solver technology to expand its solution capability and enhance Sandia’s response to problems of national importance. Current efforts include analyzing GEMMA’s response in combined environments, such as electrical and mechanical, and streamlining the GEMMA workflow.
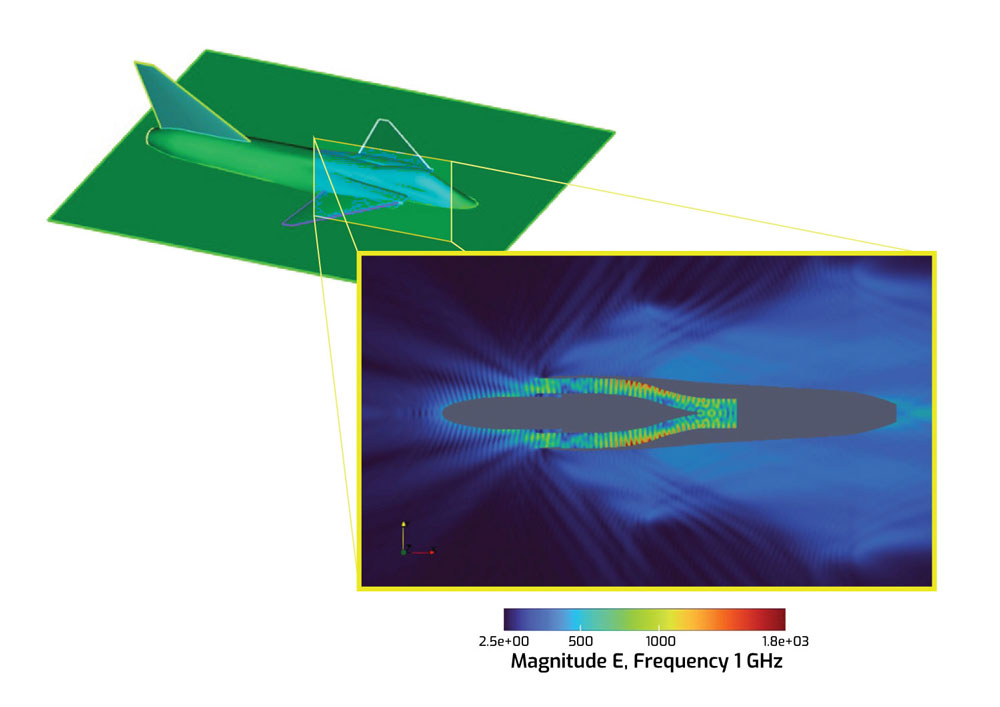
Figure 5: Magnitude of the scattered electric field on the observation plane of Figure 5.