Mapping

Applies to: Surfaces, Volumes

Summary: Meshes a surface/volume with a structured mesh of quadrilaterals/hexahedra.

Syntax:

{Volume|Surface} <range> Scheme Map

Discussion:

A structured mesh is defined as one where each interior node on a surface/volume is connected to 4/6 other nodes. Mappable surfaces contain four logical sides and four logical corners of the map; each side can be composed of one or several geometric curves. Similarly, mappable volumes have six logical sides and eight logical corners; each side can consist of one or several geometric surfaces. For example, in Figure 1 below, the logical corners selected by the algorithm are indicated by arrows. Between these vertices the logical sides are defined; these sides are described in Table 1.

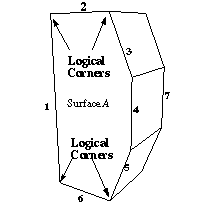
Figure 1. Scheme Map Logical Properties

Table 1. Listing of Logical Sides

Interval divisions on opposite sides of the logical rectangle are matched to produce the mesh shown in the right portion of Figure 1. (i.e. The number of intervals on logical side 1 is equated to the number of intervals on logical side 3). The process is similar for volume mapping except that a logical hexahedron is formed from eight vertices. Note that the corners for both surface and volume mapping can be placed on curves rather than vertices; this allows mapping surfaces and volumes with less than four and eight vertices, respectively. For example, the mapped quarter cylinder shown in Figure 2 has only five surfaces.

Figure 2. Volume Mapping of a 5-surfaced volume

The mapper works on a bicubic interpolation of the points on the boundary to represent the surface. There may be times that those points may not be on the surface exactly if the surface is not suitable for bicubic interpolation. The Mapping Constraint flag tells the mapper to relax the nodes to the geometry or not.

Set Mapping Constraint {ON|off}